Mathcad: A Powerful Tool for Engineering and Science

Mathcad, a powerful software tool, empowers engineers, scientists, and educators to solve complex mathematical problems, visualize data, and create interactive documents. Its intuitive interface and robust functionality make it a valuable asset in a wide range of industries and research fields.

From basic calculations to advanced simulations, Mathcad provides a comprehensive platform for mathematical exploration. It offers a seamless integration of text, equations, plots, and programming, allowing users to express their ideas and solutions in a clear and concise manner.

Introduction to Mathcad

Mathcad is a powerful software application designed for technical calculations, data analysis, and mathematical modeling. It provides a user-friendly interface that combines symbolic calculations, numerical computations, and visualization tools, enabling engineers, scientists, and mathematicians to solve complex problems and explore mathematical concepts effectively.

History of Mathcad

Mathcad was initially developed in the late 1980s by MathSoft, a company founded by a group of mathematicians and engineers. Its initial release was focused on providing a graphical interface for performing mathematical calculations and generating reports. Over the years, Mathcad has undergone significant enhancements, incorporating features such as symbolic computation, data analysis, and programming capabilities. In 2006, MathSoft was acquired by PTC, a leading provider of product lifecycle management (PLM) software, and Mathcad became part of PTC’s product portfolio.

Key Features and Functionalities

Mathcad offers a wide range of features and functionalities that make it a versatile tool for various technical applications.

• Symbolic calculations: Mathcad allows users to perform symbolic calculations, such as solving equations, finding derivatives, and integrating functions, using its built-in symbolic engine. This enables users to obtain exact solutions and gain insights into the underlying mathematical relationships.
• Numerical computations: Mathcad provides a comprehensive set of numerical computation capabilities, including matrix operations, statistical analysis, and numerical integration. Users can define variables, create arrays, and perform complex calculations with high accuracy.
• Visualization tools: Mathcad offers various visualization tools to represent data graphically, such as 2D and 3D plots, histograms, and contour plots. These visualization capabilities allow users to analyze data, identify patterns, and communicate results effectively.
• Programming capabilities: Mathcad includes a built-in programming language that allows users to create custom functions, automate tasks, and control program flow. This programming capability enhances the flexibility and power of Mathcad for solving complex problems.
• Unit support: Mathcad supports unit conversions and calculations, ensuring that calculations are performed with the correct units and that results are presented in a consistent manner.
• Data analysis: Mathcad provides tools for data analysis, including statistical functions, regression analysis, and curve fitting. These capabilities enable users to analyze data, identify trends, and draw meaningful conclusions.

Industries and Applications

Mathcad is widely used in various industries and applications, including:

• Engineering: Engineers use Mathcad for a wide range of tasks, such as structural analysis, fluid mechanics, heat transfer, and control systems design.
• Science: Scientists use Mathcad for research, data analysis, and modeling in fields such as physics, chemistry, biology, and materials science.
• Finance: Financial analysts use Mathcad for portfolio optimization, risk management, and financial modeling.
• Education: Mathcad is used in educational institutions to teach mathematics, engineering, and science concepts.
• Research and Development: Mathcad is employed in research and development for prototyping, simulation, and data analysis.

Examples of Mathcad Applications

• Solving differential equations: Mathcad can be used to solve differential equations, which are commonly encountered in physics, engineering, and other fields. For example, it can be used to model the motion of a pendulum or the flow of heat through a solid object.
• Performing statistical analysis: Mathcad can be used to perform statistical analysis on data sets, such as calculating mean, standard deviation, and correlation coefficients. This can be useful for identifying trends, making predictions, and drawing conclusions from data.
• Creating mathematical models: Mathcad can be used to create mathematical models that represent real-world systems. For example, it can be used to model the behavior of a circuit, the growth of a population, or the spread of a disease.

Mathcad Interface and Functionality

Mathcad’s user interface provides a user-friendly environment for performing mathematical calculations, creating visualizations, and documenting work. Its layout and features are designed to streamline the process of working with mathematical concepts.

Workspace Layout

The Mathcad workspace is organized into a series of regions, each with its own purpose.

• Worksheet Area: This is the main area where you enter equations, text, plots, and other elements. It resembles a traditional spreadsheet with cells for each element.
• Toolbars: These provide quick access to common commands, functions, and operators. They are located at the top of the workspace and can be customized based on user preferences.
• Menu Bar: This contains a series of menus that offer more advanced features and options, such as file management, editing, and formatting.
• Status Bar: Located at the bottom of the workspace, it displays information about the current state of the application, such as the current file name, the zoom level, and the active region.

Creating and Editing Elements

Mathcad allows you to create and edit different types of elements within the worksheet area:

• Mathematical Equations: Mathcad uses a natural mathematical notation that resembles handwritten equations. To create an equation, simply type the mathematical expression, and Mathcad automatically formats it. You can use a variety of mathematical operators, functions, and variables within your equations.
• Plots: Mathcad offers a variety of plotting options to visualize data and functions. To create a plot, you first define the data or function to be plotted, then select the desired plot type from the toolbar or menu. You can customize the appearance of the plot by adjusting its axes, labels, colors, and other properties.
• Text: You can add text to your worksheets to provide explanations, comments, or documentation. To create a text region, simply click on the worksheet area and start typing. You can format the text using the standard text editing tools available in the menu bar.

Mathematical Operations and Functions

Mathcad offers a wide range of mathematical operations and functions, covering various fields like algebra, calculus, statistics, and more.

• Basic Arithmetic Operations: Mathcad supports standard arithmetic operations like addition (+), subtraction (-), multiplication (*), division (/), and exponentiation (^). You can use these operations to perform calculations on numbers, variables, and expressions.
• Trigonometric Functions: Mathcad includes trigonometric functions like sine (sin), cosine (cos), tangent (tan), and their inverses. These functions can be used to solve problems involving angles and triangles.
• Logarithmic and Exponential Functions: Mathcad provides logarithmic functions (log, ln) and exponential functions (exp). These functions are useful for working with growth and decay models, as well as for solving equations involving exponents.
• Calculus Operations: Mathcad supports calculus operations like differentiation (d/dx) and integration (∫). These operations allow you to calculate derivatives and integrals of functions.
• Linear Algebra Functions: Mathcad offers functions for working with matrices and vectors, including operations like matrix multiplication, inversion, and determinant calculation.
• Statistical Functions: Mathcad includes a variety of statistical functions, such as mean, standard deviation, variance, and correlation coefficient. These functions are useful for analyzing data and drawing conclusions from it.

Working with Variables and Expressions

Mathcad allows you to define and manipulate variables, making it easier to work with complex mathematical expressions. This section explores the process of defining and manipulating variables, along with the use of operators and functions for mathematical calculations.

Defining and Manipulating Variables

Variables are symbolic representations of values in Mathcad. They are defined using the assignment operator (:=). The variable name should be on the left side of the assignment operator, and the value or expression to be assigned should be on the right.

For example, to define a variable ‘x’ with a value of 5, you would type:
x := 5

Once defined, variables can be used in other calculations and expressions. Mathcad will automatically substitute the value of the variable whenever it is used.

For instance, to calculate the square of ‘x’, you would type:
x^2

This will result in the value 25, as Mathcad substitutes the value of ‘x’ (5) into the expression.

Using Operators and Functions

Mathcad provides a comprehensive set of operators and functions for performing mathematical calculations. These include:

• Arithmetic Operators: +, -, *, /, ^ (addition, subtraction, multiplication, division, exponentiation)
• Relational Operators: =, ≠, <, >, ≤, ≥ (equality, inequality, less than, greater than, less than or equal to, greater than or equal to)
• Logical Operators: AND, OR, NOT (logical conjunction, logical disjunction, logical negation)
• Trigonometric Functions: sin, cos, tan, cot, sec, csc (sine, cosine, tangent, cotangent, secant, cosecant)
• Logarithmic and Exponential Functions: ln, log, exp (natural logarithm, base-10 logarithm, exponential function)
• Other Functions: sqrt, abs, round, ceil, floor (square root, absolute value, round, ceiling, floor)

Creating and Solving Equations

Mathcad allows you to create and solve equations using its built-in equation solver. To create an equation, simply type the expression and use the equality operator (=).

For example, to create the equation 2x + 5 = 15, you would type:
2x + 5 = 15

To solve the equation, you can use the ‘Solve’ function. The ‘Solve’ function takes two arguments: the equation to be solved and the variable to solve for.

To solve the equation for ‘x’, you would type:
Solve(2x + 5 = 15, x)

Mathcad will then display the solution for ‘x’, which is 5 in this case.

Creating and Customizing Plots

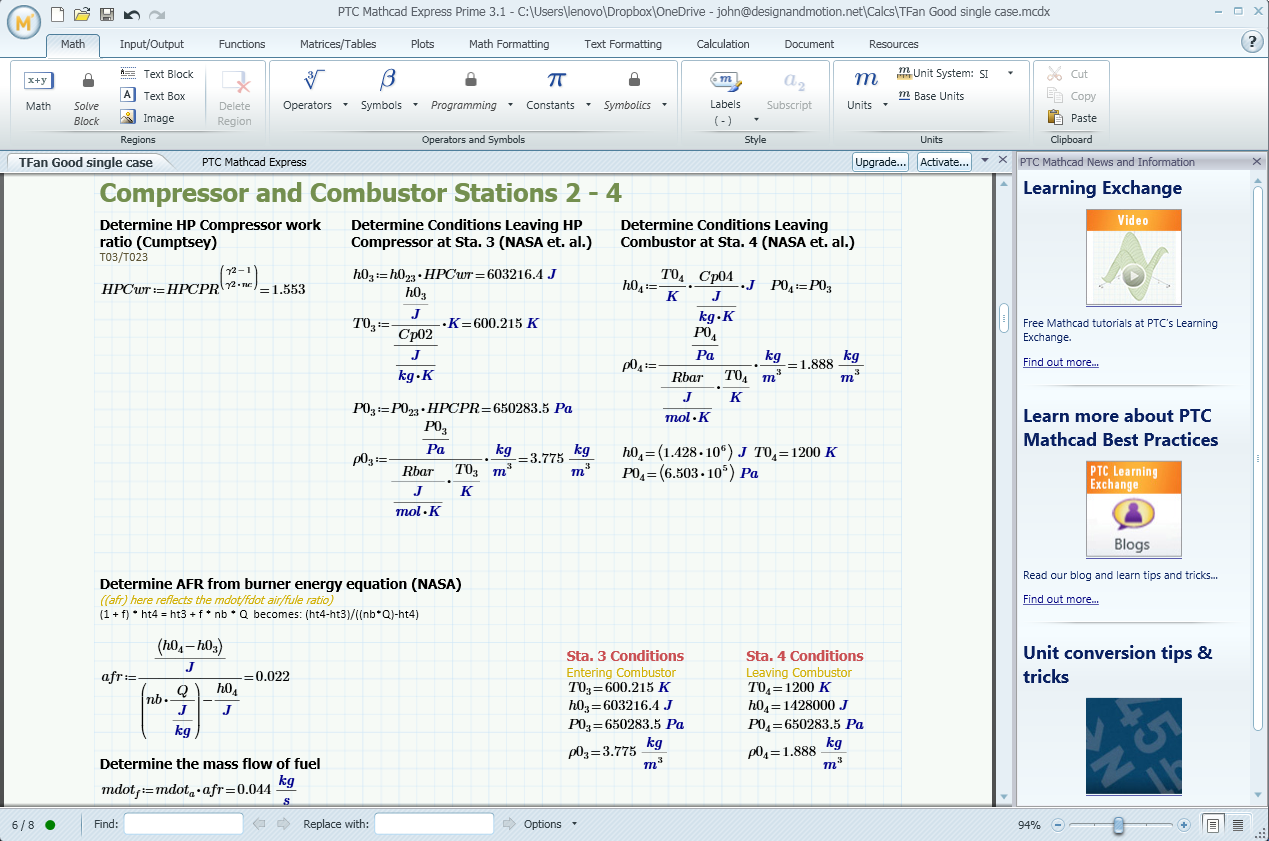
Mathcad provides a versatile plotting environment for visualizing data and exploring mathematical relationships. You can create various plot types, customize their appearance, and generate informative and visually appealing graphs.

Types of Plots

Mathcad offers a wide range of plot types, each designed for specific data visualization needs.

• X-Y Plots: These plots are used to display the relationship between two variables, where one variable is plotted against the other. They are commonly used for representing functions, data trends, and comparisons.
• Polar Plots: These plots are used to display data in polar coordinates, where points are plotted based on their distance from the origin and their angle. They are suitable for visualizing data that exhibits circular or radial patterns.
• Contour Plots: These plots are used to visualize a function of two variables by displaying lines of constant function value. They are useful for representing data with a continuous distribution, such as temperature or pressure maps.
• Surface Plots: These plots are used to visualize a function of two variables by creating a three-dimensional surface. They provide a clear visual representation of the function’s behavior over a range of input values.
• Vector Plots: These plots are used to visualize vector fields, where each point is represented by an arrow indicating the magnitude and direction of the vector. They are suitable for visualizing forces, flows, and other vector-based data.

Customizing Plot Properties

You can customize various plot properties to enhance their clarity and visual appeal.

• Axis Labels: Add labels to the x-axis and y-axis to provide context and clarity. This helps identify the variables being plotted and their units of measurement.
• Legends: Use legends to distinguish between multiple datasets or curves plotted on the same graph. Legends should be concise and informative, clearly identifying each data series.
• Colors: Choose colors that are visually distinct and contrasting to ensure clear separation between data series. Consider using color schemes that are consistent with scientific conventions or industry standards.
• Line Styles: Vary line styles, such as solid, dashed, or dotted lines, to differentiate between data series. This can enhance readability, especially when dealing with multiple datasets.
• Markers: Use markers, such as circles, squares, or triangles, to highlight data points on the plot. Markers can be customized in size, shape, and color to enhance visual clarity.

Creating Informative and Visually Appealing Plots

• Clear and Concise Labels: Use descriptive labels for axes, legends, and titles. Avoid using abbreviations or jargon that may be unfamiliar to the reader.
• Appropriate Scale: Choose an appropriate scale for the axes to ensure that all data points are visible and the relationships between them are clear. Avoid excessively large or small scales that distort the data.
• Visual Hierarchy: Use color, line styles, and markers to create a visual hierarchy that emphasizes important data points or trends.
• Data Annotations: Add annotations, such as text boxes or arrows, to highlight specific data points, trends, or features of interest.
• Consistent Formatting: Maintain consistent formatting throughout the plot, including font styles, sizes, and colors. This creates a professional and cohesive look.

Programming in Mathcad

Mathcad’s built-in scripting language allows you to create and execute programs to automate tasks, solve complex problems, and extend the capabilities of the software. This scripting language provides a powerful way to leverage the mathematical functions and tools available in Mathcad to create custom solutions.

Creating and Executing Programs

Mathcad programs are created using a combination of mathematical expressions, control flow statements, and functions. The basic building blocks of a Mathcad program are:

* Variables: Variables are used to store values that can be manipulated within the program.
* Operators: Mathcad provides a wide range of operators for performing arithmetic, logical, and relational operations.
* Functions: Functions allow you to encapsulate a sequence of instructions into a reusable block of code.
* Control Flow Statements: Control flow statements like “if” statements and loops allow you to control the execution flow of your program.

Loops

Loops are used to repeat a block of code a specific number of times or until a certain condition is met. Mathcad supports several types of loops, including:

* For Loops: A “for” loop executes a block of code a predetermined number of times.

For i = 1 to 10

x[i] := i^2

Next i

This loop assigns the square of the loop counter (i) to the variable x[i], iterating from 1 to 10.

* While Loops: A “while” loop executes a block of code as long as a specified condition remains true.

i := 1

While i < 10 x[i] := i^2 i := i + 1 End While

This loop assigns the square of the loop counter (i) to the variable x[i], iterating as long as i is less than 10.

Conditional Statements

Conditional statements allow you to execute different blocks of code based on the result of a logical condition. The most common conditional statement is the “if” statement:

If condition then

// Code to execute if condition is true

Else

// Code to execute if condition is false

End If

For example, you could use an “if” statement to determine whether a number is positive, negative, or zero:

x := -5

If x > 0 then

Print(“x is positive”)

Elseif x < 0 then Print(“x is negative”) Else Print(“x is zero”) End If

Functions

Functions allow you to group a set of instructions into a reusable block of code that can be called with different inputs. They are defined using the “function” followed by the function name, input parameters, and the code block to be executed:

function MyFunction(x, y)

return x + y

End Function

This function, named “MyFunction,” takes two input parameters, “x” and “y,” and returns their sum. You can then call this function within your program:

result := MyFunction(3, 5)

Print(result)

This code will call the “MyFunction” function with inputs 3 and 5, store the result in the variable “result,” and then print the value of “result” (which will be 8).

Automating Tasks and Solving Complex Problems

Mathcad programs can automate repetitive tasks, perform complex calculations, and analyze data. For example, you could create a program to:

* Calculate the average of a list of numbers:

// Define a list of numbers

numbers := 1, 2, 3, 4, 5

// Calculate the sum of the numbers

sum := 0

For i = 1 to 5

sum := sum + numbers[i]

Next i

// Calculate the average

average := sum / 5

// Print the average

Print(“The average is:”, average)

* Solve a system of linear equations:

// Define the coefficients of the equations

A := 2, 1, 1, 3

b := 5, 7

// Solve the system of equations

x := Solve(A, b)

// Print the solution

Print(“The solution is:”, x)

* Generate a table of data:

// Define the range of values for x

x := 0, 0.1..1

// Calculate the corresponding values for y

y := x^2

// Create a table of x and y values

Table(x, y)

These are just a few examples of how Mathcad programming can be used to automate tasks and solve complex problems. With its powerful scripting language and integrated mathematical functions, Mathcad provides a versatile platform for creating custom solutions tailored to your specific needs.

Mathcad and Data Analysis

Mathcad is a powerful tool for data analysis, providing a comprehensive environment for importing, manipulating, and visualizing data, as well as performing statistical analysis. It simplifies the process of extracting insights from data and allows for clear communication of findings.

Importing and Exporting Data, Mathcad

Mathcad offers various methods for importing and exporting data. Users can import data from various sources, including spreadsheets, databases, text files, and web pages.

• Importing data from spreadsheets: Mathcad can directly import data from Excel, CSV, and other spreadsheet formats. Users can select specific ranges or entire worksheets.
• Importing data from text files: Mathcad supports importing data from plain text files, allowing users to import data separated by delimiters like commas, tabs, or spaces.
• Importing data from databases: Mathcad can connect to databases using ODBC drivers and retrieve data based on specific queries.
• Importing data from web pages: Mathcad can import data from web pages, including tables and data presented in various formats.

Mathcad also allows users to export data in various formats, including spreadsheets, text files, and images, facilitating data sharing and further analysis.

Data Manipulation

Mathcad provides a range of tools for manipulating data. Users can perform various operations, including sorting, filtering, and transforming data.

• Sorting data: Mathcad allows users to sort data based on specific columns or rows, enabling organization and analysis.
• Filtering data: Users can filter data based on specific criteria, isolating relevant data points for analysis.
• Transforming data: Mathcad offers various functions for transforming data, including calculations, statistical operations, and data aggregation.

These data manipulation features enable users to prepare data for further analysis and visualization.

Statistical Analysis

Mathcad offers a comprehensive suite of statistical functions and tools for analyzing data.

• Descriptive statistics: Mathcad calculates various descriptive statistics, including mean, median, standard deviation, variance, and percentiles, providing insights into the central tendency and variability of data.
• Hypothesis testing: Mathcad enables users to perform hypothesis tests, such as t-tests, z-tests, and ANOVA, to assess the significance of differences between groups or populations.
• Regression analysis: Mathcad supports linear and non-linear regression analysis, allowing users to model relationships between variables and predict future outcomes.
• Correlation analysis: Mathcad calculates correlation coefficients, quantifying the strength and direction of linear relationships between variables.

These statistical analysis capabilities empower users to draw meaningful conclusions from data and support decision-making.

Examples of Data Analysis using Mathcad

• Analyzing sales data: Users can import sales data from a spreadsheet, perform calculations like total sales, average sales, and sales growth, and create visualizations like bar charts and line graphs to analyze sales trends over time.
• Evaluating student performance: Educators can import student test scores, calculate descriptive statistics, and perform hypothesis tests to assess the effectiveness of teaching methods or identify areas for improvement.
• Predicting market trends: Financial analysts can import stock prices, perform regression analysis to model price movements, and predict future stock prices based on historical data.

Integration with Other Software

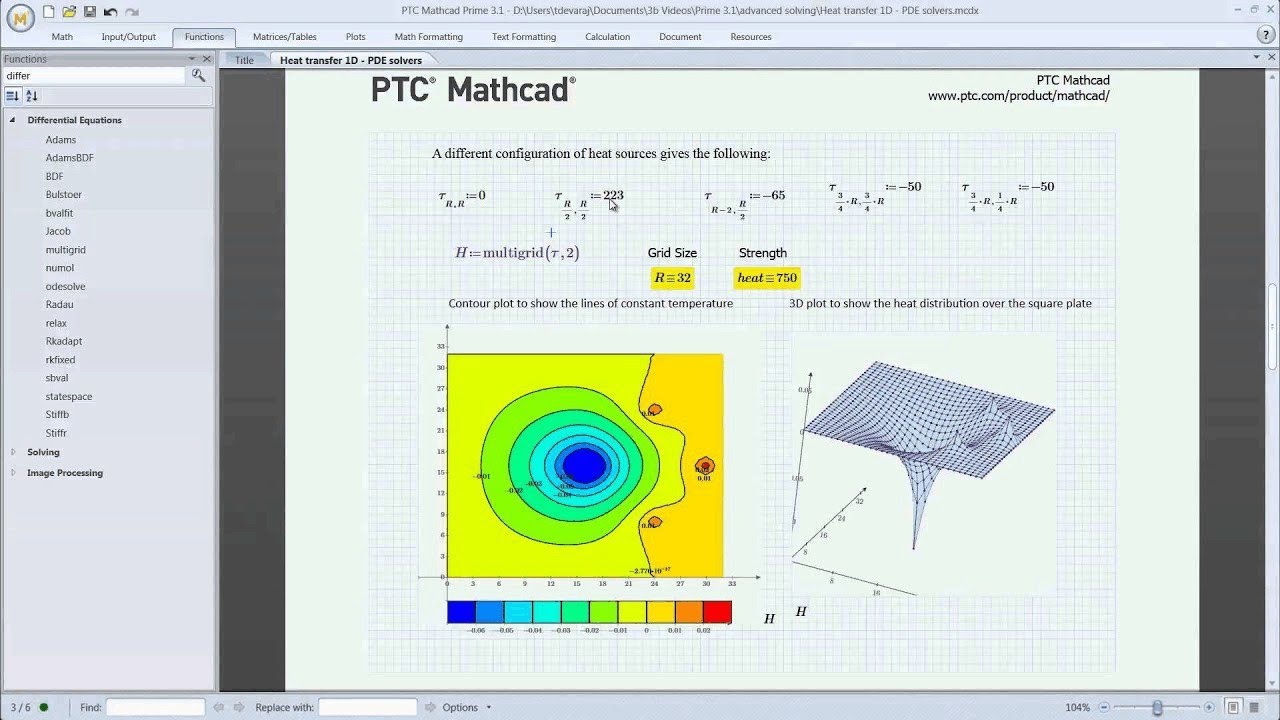
Mathcad’s strength lies in its ability to seamlessly integrate with other software applications, enhancing its capabilities and enabling a wider range of tasks. This integration allows for data exchange, collaborative work, and leveraging the strengths of different tools.

Integration with Spreadsheets

Mathcad offers powerful tools for data manipulation and analysis, but it also recognizes the importance of working with spreadsheets. Mathcad allows you to import data from spreadsheets like Microsoft Excel, Google Sheets, or OpenOffice Calc. This import process can be done directly by using the “Insert” menu or by utilizing the “Read” function. Once imported, you can perform calculations, create plots, and analyze the data within Mathcad. You can also export data from Mathcad to a spreadsheet, allowing you to further process or share the results.

The seamless integration with spreadsheets makes Mathcad a valuable tool for engineers, scientists, and financial analysts who frequently work with large datasets.

Integration with Programming Languages

Mathcad allows you to interact with various programming languages like C, C++, Java, Python, and MATLAB. This integration provides a powerful way to extend Mathcad’s capabilities and utilize existing code. You can use Mathcad to call functions from these programming languages, allowing you to perform complex calculations or simulations within Mathcad. You can also embed Mathcad code within a larger program written in a programming language.

This integration allows you to combine the ease of use of Mathcad with the power and flexibility of programming languages.

Integration with CAD Software

Mathcad can be used to create and analyze models created in CAD software. You can import CAD files into Mathcad and use the software’s built-in tools to perform calculations and simulations on the model. This integration is especially useful for engineers who need to analyze the behavior of structures or components under different conditions.

Mathcad’s integration with CAD software provides a powerful tool for engineers and designers to analyze and optimize their designs.

Collaboration and Sharing

Mathcad supports collaborative work by allowing users to share their workbooks with others. Users can work on the same workbook simultaneously, making it easier to share data and results. Mathcad also offers the ability to export workbooks in various formats, including HTML, PDF, and Word, making it easy to share results with colleagues or clients.

This collaboration and sharing feature allows for seamless project management and efficient communication among team members.

Real-World Applications of Mathcad

Mathcad is a powerful tool that can be used to solve a wide range of problems in various fields. Its versatility and ease of use make it a valuable asset for engineers, scientists, financial analysts, educators, and many others.

Engineering

Mathcad’s capabilities in engineering are extensive, encompassing a broad range of applications.

• Structural Engineering: Mathcad is used to analyze and design structures, such as bridges, buildings, and aircraft. For example, engineers can use Mathcad to calculate the stresses and strains in a beam under different loading conditions.
• Mechanical Engineering: Mathcad is used to model and simulate mechanical systems, such as engines, turbines, and robots. Engineers can use Mathcad to analyze the performance of these systems and optimize their design.
• Electrical Engineering: Mathcad is used to design and analyze electrical circuits, such as power systems, communication networks, and control systems. Engineers can use Mathcad to calculate the current, voltage, and power in a circuit.
• Chemical Engineering: Mathcad is used to model and simulate chemical processes, such as distillation, filtration, and reaction kinetics. Engineers can use Mathcad to optimize the design of these processes and predict their performance.

Science

Mathcad’s application in science is equally significant, providing researchers with tools to model, analyze, and visualize scientific data.

• Physics: Mathcad is used to solve complex physics problems, such as those involving mechanics, electromagnetism, and thermodynamics. Scientists can use Mathcad to calculate the motion of objects, the forces acting on them, and the energy they possess.
• Chemistry: Mathcad is used to model and simulate chemical reactions, such as those involving acids, bases, and redox reactions. Chemists can use Mathcad to predict the products of reactions, their rates, and their equilibrium constants.
• Biology: Mathcad is used to analyze biological data, such as population growth, gene expression, and protein structure. Biologists can use Mathcad to model the behavior of biological systems and identify patterns in their data.

Finance

Mathcad’s ability to handle complex calculations and financial models makes it a valuable tool in finance.

• Financial Modeling: Mathcad is used to create financial models that can be used to forecast future financial performance, analyze investment opportunities, and assess risk.
• Portfolio Management: Mathcad is used to optimize investment portfolios by calculating the expected return and risk of different asset classes.
• Valuation: Mathcad is used to value companies and assets using various valuation models, such as discounted cash flow analysis.

Education

Mathcad plays a crucial role in education by enhancing the learning experience and fostering a deeper understanding of mathematical concepts.

• Teaching and Learning: Mathcad is used by educators to illustrate mathematical concepts, solve problems, and create interactive learning materials.
• Student Projects: Mathcad is used by students to complete assignments, research projects, and develop their problem-solving skills.
• Research: Mathcad is used by researchers to analyze data, develop models, and communicate their findings.

Mathcad for Education and Research

Mathcad has become an indispensable tool in the world of education and research, empowering students, educators, and researchers alike to explore, visualize, and communicate mathematical concepts with ease. Its intuitive interface, powerful calculation capabilities, and seamless integration with other software make it an ideal platform for both teaching and advanced research projects.

Using Mathcad for Teaching and Learning Mathematics

Mathcad’s ability to seamlessly blend mathematical notation, text, and graphical representations makes it a powerful tool for teaching and learning mathematics.

• Interactive Tutorials: Mathcad can be used to create interactive tutorials that allow students to explore mathematical concepts in a hands-on manner. For example, a tutorial on derivatives could allow students to manipulate a function and observe how its derivative changes in real-time. This interactive approach can enhance student engagement and understanding.
• Visualizing Complex Concepts: Mathcad excels at visualizing complex mathematical concepts, making them more accessible to students. For instance, 3D plots can be used to represent multivariable functions, helping students grasp the relationships between variables in a more intuitive way.
• Problem Solving and Exploration: Mathcad allows students to solve problems and explore mathematical concepts in a more engaging and interactive way. Students can easily input formulas, manipulate variables, and see the results in real-time, fostering a deeper understanding of the underlying principles.

Utilizing Mathcad for Research and Development Projects

Mathcad’s versatility and power extend beyond the classroom, making it a valuable tool for researchers and developers across various disciplines.

• Data Analysis and Modeling: Researchers can use Mathcad to analyze large datasets, perform statistical analysis, and develop mathematical models to represent real-world phenomena. Its robust capabilities for data manipulation, curve fitting, and statistical analysis make it ideal for quantitative research.
• Simulation and Optimization: Mathcad’s programming capabilities enable researchers to build simulations and optimize complex systems. For example, engineers can use Mathcad to simulate the performance of a new design or optimize the parameters of a manufacturing process.
• Collaboration and Communication: Mathcad facilitates collaboration and communication within research teams by providing a platform for sharing results, calculations, and models. Its ability to integrate with other software, such as spreadsheets and presentation programs, further enhances its usefulness for research projects.

Creating Interactive Tutorials with Mathcad

Mathcad’s ability to combine mathematical notation, text, and graphical representations allows for the creation of dynamic and engaging tutorials.

• Interactive Examples: Mathcad can be used to create interactive examples that allow students to explore mathematical concepts by manipulating variables and observing the resulting changes. For instance, a tutorial on linear equations could allow students to adjust the slope and intercept of a line and see how these changes affect the equation and its graph.
• Step-by-Step Solutions: Mathcad can provide step-by-step solutions to problems, guiding students through the process of solving them. This approach can be particularly helpful for students who are struggling with a particular concept or technique.
• Visual Feedback: Mathcad can provide visual feedback to students as they work through a tutorial. For example, if a student enters an incorrect answer, the software can highlight the error and provide a suggestion for correction. This type of immediate feedback can help students learn from their mistakes and improve their understanding.

Visualizing Complex Concepts Using Mathcad

Mathcad’s graphical capabilities make it an ideal tool for visualizing complex mathematical concepts, enhancing student understanding and comprehension.

• 3D Plots: Mathcad’s 3D plotting capabilities allow researchers and educators to visualize multivariable functions, providing a deeper understanding of the relationships between variables. This can be particularly helpful in fields like physics, engineering, and economics, where complex relationships are often encountered.
• Animations: Mathcad can be used to create animations that illustrate the behavior of mathematical functions over time. This can be helpful in understanding concepts like calculus, where the rate of change of a function is crucial.
• Interactive Graphs: Mathcad allows users to create interactive graphs where students can manipulate variables and see the resulting changes in the graph in real-time. This interactive approach can be highly engaging and help students develop a deeper understanding of the relationships between variables.

The Future of Mathcad

Mathcad has been a mainstay in the world of engineering and science for decades, providing a powerful and user-friendly platform for calculations, simulations, and data analysis. As technology continues to evolve, Mathcad is poised to play an even more significant role in the future, adapting to the changing needs of its users and embracing emerging trends.

Impact of Emerging Technologies

The rise of cloud computing, artificial intelligence (AI), and machine learning (ML) is transforming the way we interact with technology. Mathcad is well-positioned to leverage these advancements, offering a more collaborative, intelligent, and efficient user experience.

• Cloud Integration: Mathcad could be integrated with cloud platforms, allowing users to access their work from anywhere, collaborate with colleagues in real-time, and share their results seamlessly. This would enable a more dynamic and accessible approach to problem-solving, breaking down geographical barriers and fostering collaboration.
• AI-Powered Assistance: AI algorithms can be incorporated into Mathcad to provide intelligent assistance to users, such as suggesting relevant functions, identifying errors, and even automating repetitive tasks. This would enhance user productivity and allow users to focus on higher-level problem-solving.
• Machine Learning for Data Analysis: Mathcad could leverage ML algorithms to analyze complex datasets, identify patterns, and generate insights. This would empower users to make data-driven decisions and gain a deeper understanding of their data.

Future Role of Mathcad in Engineering and Science

As technology advances, Mathcad is likely to play a more central role in various engineering and scientific fields. Here are some key areas where Mathcad’s influence will likely grow:

• Simulation and Modeling: With the increasing complexity of engineering systems, the need for accurate and sophisticated simulations is growing. Mathcad can be used to create detailed models of these systems, allowing engineers to test different designs, optimize performance, and predict outcomes.
• Data-Driven Design: As data becomes more readily available, engineers are increasingly relying on data-driven design principles. Mathcad can be used to analyze large datasets, identify trends, and inform design decisions. This will enable engineers to create more efficient and effective designs.
• Education and Research: Mathcad will continue to be an invaluable tool for students and researchers, providing a platform for learning, exploration, and discovery. Its user-friendly interface and powerful capabilities make it ideal for teaching fundamental concepts and conducting complex research.

Predictions about the Future of Mathcad

While predicting the future is inherently challenging, several trends suggest that Mathcad is well-positioned for continued growth and innovation.

• Increased User Base: As more students, engineers, and scientists embrace Mathcad, the user base is likely to grow significantly. This will create a larger community of users, leading to more shared resources, tutorials, and collaboration opportunities.
• Enhanced Functionality: Mathcad will likely continue to evolve, incorporating new features, functions, and capabilities to meet the changing needs of its users. This will ensure that Mathcad remains a cutting-edge tool for problem-solving and analysis.
• Integration with Other Software: Mathcad will likely become more integrated with other software applications, such as CAD programs, data analysis tools, and simulation platforms. This will enable users to work seamlessly across different software environments, streamlining workflows and improving productivity.

Closure

As technology continues to evolve, Mathcad remains at the forefront of mathematical software, adapting to new challenges and providing innovative solutions. Whether you’re a seasoned professional or a budding student, Mathcad offers a powerful and versatile tool to enhance your understanding of mathematics and its applications in the real world.

Mathcad is a powerful tool for engineers and scientists, allowing them to perform complex calculations and create interactive documents. If you’re looking to take your Mathcad projects to the next level, consider using a free app maker to create a mobile or web application that integrates your calculations and visualizations.

This can make your work more accessible and engaging for colleagues and clients.